Computing Instrument Settings from Instrument Specifications
This article will explain the most commonly used methods for computing instrument standard errors, or "Instrument Settings" for STAR*NET. An online calculator that applies these formulas is available here.
Important Points:
- Direction Setting weights direction sets (DB, DN, DE combinations) and DV
- Direction Setting can be set a number of ways:
- Determine by field testing
- Use the Manufacturer’s DIN 18723 * √2 See here for more information.
- Use the Manufacturer’s ISO 17123-3 * √2
- Angle Setting weights M, SS, A measurements.
- Angular settings can be determined from field testing
- Angular settings can be calculated as shown below
- Azimuth/Bearing weights B and BM measurements
- Distance and constant settings weight D, DV or any distance component
- Zenith and Vertical Difference settings are derived from direction setting and (sometimes) distance constant.
- NOTE: Vertical Difference Settings only need to be entered when the "Distance/Vertical Data Type" option on the General tab of project settings is set to "Horiz Dist / Elev Diff"
- Centering affects most measurements
|
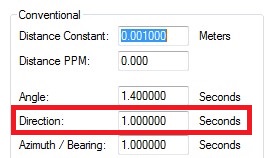
Direction Accuracy can be computed from Instrument Specification: DIN 18723 Specification for Theodolite Accuracy (i.e. a “1 second instrument”)applies to a repeated F1 and F2 “Pointing” or target sighting (ISO 17123 Specification is the same for practical purposes.) 1. Compute Direction setting given:
Direction Std Err for a single direction = DIN 18723 (or ISO 17123) multiplied by √2. See here for more information. Eg: 1 observations with a 1 second instrument: 1”*√2 = 1.414” Or if direction is averaged from N observations: Direction Std Error = DIN 18723*√2 / √ N Eg: 2 observations with a 5 second instrument: 5”*√ 2 / √ 2 = 5” Eg: 6 observations with a 2 second instrument: 2”*√2 / √ 6 =1.15” |
 |
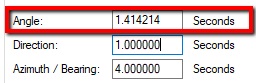
| Angular Accuracy: 2. Compute Angular Std Err from Direction Std Error computed above Angular Std Err= √(Direction²+Direction²) E.g.: (1 FS + 1 BS) with a 1 second instrument: √(1.414"²+1.414"² ) = 2" E.g.: (2 FS + 2 BS) with a 5 second instrument: √(5"²+5"² ) = 7.07" |
 |
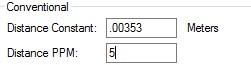
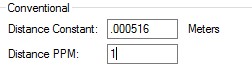
| Distance Accuracy Given as the Constant and PPM values generated when the EDM was calibrated. When multiple observations are averaged the constant must be calculated: Where: Constant = Given EDM Constant PPM = Given ppm constant divided by 1 million N = number of distance measurements averaged Distance Constant = Constant/ √N PPM is as given, it is not affected by averaging Eg.: EDM with PPM = 5, constant = .005 meters averaging 2 measurements: Constant = .005m / √2 = .00353m, PPM = 5 Eg: EDM with PPM = 1, constant = .002 meters averaging 15 measurements: Constant = .002m /√15 = .000516 meters, PPM = 1 |
NOTES:
  |
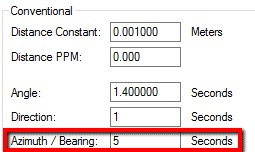
| Azimuth/Bearing Directional accuracy to be applied to given directions, gyroscopic or astronomical observations. |
 |
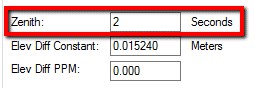
| Zenith 2. Compute Zenith Std Error from Direction Std Error computed above. Typically 2 x the Direction Std Error Std Error = (Direction*2) Eg: 1 observation with a 1 second instrument: 2 * 1.414” = 2.828” Eg: 6 observations with a 2 second instrument: 2 * 1.15” = 2.31” |
 |
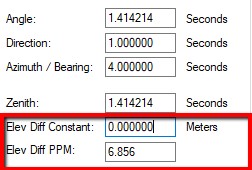
| Elev Diff Constant and Elev Diff PPM ONLY takes effect if you are manually entering 3D data in the form of horizontal distances and vertical differences. Not used very often. Elev Diff Constant: use your judgement, it just has to be non-zero Elev Diff PPM: if Elev Diff was computed from zenith observations and slope distances you can derive a PPM after computing the zenith value above. PPM=sin(zenith)*1000000 Eg: 2 observations with a 1 second instrument: Sin(2”)*1000000 = 9.696 PPM Eg: 6 observations with a 2 second instrument: Sin(2.309”)*1000000 = 11.196 PPM Elev Diff PPM values applied to elev diff input compare well to zenith values applied to zenith/slope distance input for computed Z standard deviations in the listing when slopes are shallow, but are less effective for steep observations. |
NOTES:
 |
|
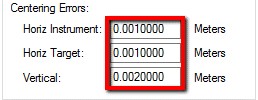
Centering Errors Horiz. Instrument: How well is the instrument centered over the mark? Horiz. Target: How well is a target prism centered over the mark?
|
 |

James Johnston
Comments