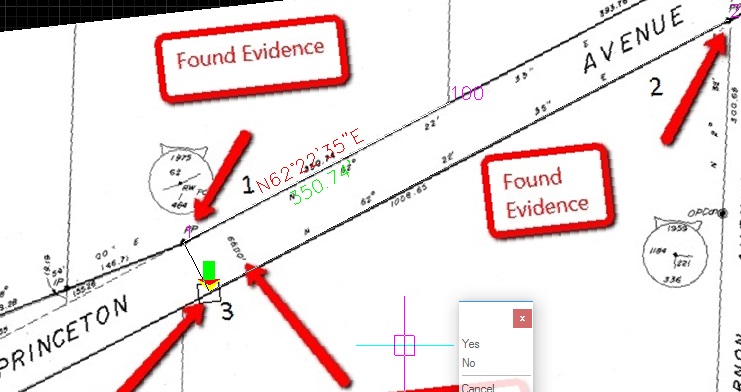
MicroSurvey's COGO routines can be used to solve many geometry problems to reconstruct lots from evidence. In the scenario below, the road width is a known, and two Pipe Posts have been found, one on the southerly side and one on the northerly side of the road.
In the example above we can see that Pipe Posts 1 and 2 have been found. The Highways plan tells us the road width is defined as exactly 66 feet.
Follow the steps below to solve for the location of 3 opposite point 1:
1. Turn off "Draw Lines/Curves" in Hot Toggles
2. Start the COGO Command:
Command: COGO
Inverse:Pt..Pt/Curve Inverse:Pt..Pt..Pt
3. Start at Point 1:
Enter From Point: <3>(Backup/Toggles/Curve/CB): 1
Options: +/- or Pt..Pt+-Angle
4. Since we don't know the direction to the point opposite 1 (unknown point 3) we hit "Enter:"
Enter Quadrant Bearing (QDD.MMSS):<>: (Backup Toggles Points Line): Hit "Enter" here as this is unknown
Options: C#=-*/sin/cos/tan... or Pt..Pt(+-*/) a Distance
5. Now we enter "66" as the known distance:
Enter the Distance: <>:(Backup Toggles Points Line): 66
-->Distance used = 66.000000
6. Now we tell the routine to create Point 3 when we are finished:
Pick or Enter the Solve Point: <3>(Backup Toggles)3
Options: C#=-*/sin/cos/tan... or Pt..Pt(+-*/) a Distance
Enter Distance2: <>:(Backup Toggles Points Line Repeat):
7. Now the routine has determined that this is an angle offset scenario, so prompts you for an angle. You can enter 90 or 270 in this situation as you will be presented with both possible solutions:
Enter Angle for Distance/Angle: <>DDD.MMSS (or Point / Line): 270 (enter 270 or 90)
8. Identify the "To" point; which is the other known point, as 2:
Pick or Enter the To Point: <2>:2
Point :3 North : 1353.484 East : 1488.144
9. Pick "N" if the presented solution is wrong, and "Y" when it is correct:
Do you want to use this solution (Yes/No) (No for other solution) Y
You will be shown the two possible solutions, enter "Y" when you see the correct solution
1 S27°39'20"E dist= 66.000 N= 1353.484 E= 1488.144 3
Enter Description:<>: Corner
Stored #3
10. Point 3 is stored.

James Johnston
Comments